The word "OR" equals?
"Add" (steak OR chicken OR salmon) = (1 + 1+ 1) = 3 choices
The word "AND" equals?
"Multiply" (steak OR chicken OR salmon) AND (soup OR salad) = (1 + 1 + 1) × (1 + 1) = 3 choices × 2 choices = 6 choices
The number of ways of arranging n distinct objects, if there are no restrictions...
n! (n factorial) Refers to the product of all the integers from 1 to n, inclusive. 3! = 3×2×1 = 6 There are 6 uniquely-shaped objects on a table, how many ways can the objects be ordered in a row? 6! = 6×5×4×3×2×1 = 720
If m members of a group are identical, divide the total number of arrangements by...
m! How many ways can you arrange the letters in the word EEL? 3 letters total = 3! 2 letters are identical (repeating set) = 2! 3! / 2! = 6/2 = 3 possible ways
7 people enter a race. There are 4 types of medals awarded. The winner gets a platinum medal, the runner-up gets a gold medal, the next two racers each get a silver medal, and the last 3 racers all get bronze medals. What is the number of different ways the medals can be awarded?
7 racers total = 7! 1 gets platinum medal 1 gets gold medal 2 get silver medals (repeating set) = 2! 3 get bronze medal (repeating set) = 3! 7! / 3!2! = (7×6×5×4×3×2×1) / (3×2×1×2×1) = 7×6×5×4 / 2 = 840/2 = 420
An office manager must choose a five-digit lock code for the office door. The first and last digit must be odd, and no repetition of digits is allowed. How many lock codes are possible?
The first digit of the lock code can be 1 or 3 or 5 or 7 or 9. 5 odd digits possible for the FIRST number. 4 odd digits possible for the LAST number 5 × ___ × ___ × ___ × 4 8 total digits possible for 2nd digit 7 total digits possible for 3rd digit 6 total digits possible for 4th digit 5 × 8 × 7 × 6 × 4 = 6,720
Single group: A local card club will send 3 representatives to the national conference. If the local club has 8 members, how many different groups of representatives could the club send?
8 members total = 8! 3 members to be chosen (repeating set) = 3! 5 members not being chosen (repeating set) = 5! 8!/5!3! = (8×7×6×5×4×3×2×1) / (5×4×3×2×1×3×2×1) = 8×7×6 / 3×2×1 = (8 × 7 × 6)/ 6 = 8 × 7 = 56
Single group (Using an Anagram Grid): A local card club will send 3 representatives to the national conference. If the local club has 8 members, how many different groups of representatives could the club send?
Single group (Using an Anagram Grid): A local card club will send 3 representatives to the national conference. If the local club has 8 members, how many different groups of representatives could the club send?
8!/5!3! = (8×7×6×5×4×3×2×1) / (5×4×3×2×1×3×2×1) = 8×7×6 / 3×2×1 = (8 × 7 × 6)/ 6 = 8 × 7 = 56
Multiple groups: The I Eta Pi fraternity must choose a delegation of three senior members and two junior members for an annual fraternity conference. If I Eta Pi has 6 seniors and 5 junior members, how many delegations are possible?
6 seniors total = 6! 3 members to be chosen (repeating set) = 3! 3 members not being chosen (repeating set) = 3! 6! / 3!3! = (6×5×4×3×2×1) / (3×2×1×3×2×1) = 6×5×4 / 2 = 20 3 juniors total = 5! 2 members to be chosen (repeating set) = 2! 3 members not being chosen (repeating set) = 3! 5! / 3!2! = (5×4×3×2×1) / (3×2×1×2×1) 5×4 / 2 = 10 20 seniors AND 10 juniors 20 × 10 = 200 possible delegations ***Remember that AND means MULTIPLY
Single group, multiple decisions: A committee must choose a color scheme. There are seven non-repeating colors to choose from. How many color schemes are possible if the committee can select at most 2 colors?
Note the words "at most 2 colors". The committee can select 1 color from 7 for the scheme or 2 colors from 7. Select a 1 color scheme: 7 colors total = 7! 1 color chosen = 1! 6 colors not chosen = 6! 7! / 6!1! = 7×6×5×4×3×2×1 / 6×5×4×3×2×1×1 = 7 / 1 = 7 Select a 2 color scheme: 7 colors total = 7! 2 color chosen = 2! 5 colors not chosen = 5! 7! / 5!2! = 7×6×5×4×3×2×1 / 5×4×3×2×1×2×1 = 7 × 6 / 2 = 42/2 = 21 7 OR 21 = 7 + 21 = 28 possible color schemes ***Remember that OR means ADD
In how many different ways can the letters in the word "LEVEL" be arranged?
Total letters in "LEVEL" = 5! Number of times "L" repeats = 2! Number of times "E" repeats = 2! 5! / 2!2! = 120/4 = 30
There are an unlimited supply of 5 different types of truffles. If each box holds 2 truffles of different types, how many different boxes can be made?
Total types of truffles = 5! Number of types that can be chosen for each box = 2! Number of types that can't be chosen for each box = 3! 5! / 3!2! = (5×4×3×2×1)/(3×2×1×2×1) = 5×4 / 2 = 20/2 = 10
A store uses 4 different ingredients for their trail mix. How many bins will be needed to hold every possible blend, assuming that each blend must have at least two ingredients? (Also assume that each bin can hold one and only one blend.)
***Note that each blend must have at least two ingredients. Total ingredients = 4! Blends with 2 ingredients = 2 chosen and 2 not chosen = 2!2! Blends with 3 ingredients = 3 chosen and 1 not chosen = 3!1! Blends with 4 ingredients = 4! chosen 4! / 2!2! = 24/4 = 6 unique blends 4! / 3!1! = 24/6 = 4 unique blends 4! / 4! = 24/24 = 1 unique blend 6 + 4 + 1 = 11 blends. Therefore, 11 bins needed.
Mario's pizza has two choices of crust, five choices of toppings, and two choices of cheese. How many different choices are possible if a 4-topping pizza is ordered?
Total number of toppings = 5! Number of toppings ordered = 4! Total types of crust = 2! Total types of cheese = 2! Toppings ordered out of those available: 5!/4! = 5 Total number of choices = 5 toppings × 2 crusts × 2 cheeses = 20
A pod of 6 dolphins always swims single file, with 3 females at the front and 3 males in the rear. In how many different arrangements can the dolphins swim?
The question states that the groups of male and female dolphins will never switch positions. Total arrangements that female dolphins can swim = 3! Total arrangements that males dolphins can swim = 3! F1 F2 F3 M1 M2 M3 or F2 F3 F1 M2 M3 M1, etc 3! (females) AND 3! (males) = 6 AND 6 = 6×6 = 36
What is the probability that, on three rolls of a 6-sided die, at least one of the rolls will be a 6?
Calculate the possibility that none of the rolls are a 6. For each of the three rolls, there is a 5/6 probability that the die will not yield a 6. 1 - x 1 - (5/16 ∗ 5/16 ∗ 5/16) = (216/216) - (125/216) = 91/216
If Alicia only walks South or East on her way to work, how many possible routes can she take to work?
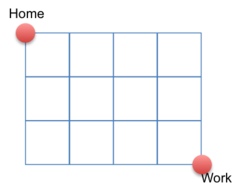
If Alicia only walks South or East on her way to work, how many possible routes can she take to work?
Total blocks = 7 → 7! Decisions to go East = 4 → 4! Decisions to go South = 3 →3! ------ 7!/4!3! = 35
Glue Method: Greg, Marcia, Peter, Jan, Bobby, and Cindy go to a movie and sit in 6 adjacent seats. If Marcia and Jan won't sit next to each other, in how many different arrangements can the 6 people sit together?
Solve problem as usual: 6! = 720 different arrangements ---------- Glue method: "Glue" Jan and Marcia together. Now there are only 5 people → 5! = 120 different arrangements ---------- Marcia and Jane can be arranged at M-J or J-M so 120(2) = 240 ---------- 720 - 240 = 480 different arrangements
Probability Tree: Jeff has a bag of 6 candies, 4 sweet and 2 sour. Jack picks two candies. What is the chance that exactly one of the candies is sour?
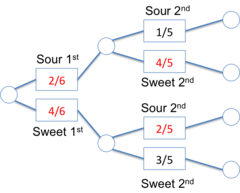
Probability Tree: Jeff has a bag of 6 candies, 4 sweet and 2 sour. Jack picks two candies. What is the chance that exactly one of the candies is sour?
Sour then Sweet = (2/6) × (4/5) = 8/30 or Sweet then Sour = (4/6) × (2/5) = 8/30 --------------- Either way the probability is the same.
Combinatorics and Domino Effect: A gumball machine contains 7 blue, 5 green, and 4 red gumballs. If the machine dispenses three gumballs at random, what is the probability at it dispenses one gumball of each color?
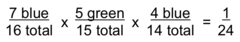
Combinatorics and Domino Effect: A gumball machine contains 7 blue, 5 green, and 4 red gumballs. If the machine dispenses three gumballs at random, what is the probability at it dispenses one gumball of each color?
3 ways the gumballs can be dispensed = 3! 3!(1/24) = 6(1/24) = 1/4
Gordon bought 5 dolls for his 5 nieces. Two GI Jane, one Josie, one Jacky, and one Rhonda. If one niece doesn't want the Rhonda doll, in how many different ways can he give the gifts?
5 dolls = 5! 2 duplicates (GI Janes) = 2! 5!/2! = 60 ------------- One niece doesn't want Rhonda so remove the niece 4!/2! = 12 ------------- 60 - 12 = 48 different ways
1! =
1
2! =
2
3! =
6
4! =
24
5! =
120
6! =
720
In how many different ways can the letters in the word
In how many different ways can the letters in the word "LEVEL" be arranged?
30
Amy and Adam are making boxes of truffles to give out as wedding favors. They have an unlimited supply of 5 different types of truffles. If each box holds 2 truffles of different types, how many different boxes can they make?
Amy and Adam are making boxes of truffles to give out as wedding favors. They have an unlimited supply of 5 different types of truffles. If each box holds 2 truffles of different types, how many different boxes can they make?
Combinación en grupos donde el orden no importa. Nos da igual sacar la Trufa 1 primero y la Trufa 3 segundo que la Trufa 3 y luego la Trufa 1. La cesta una vez puesta a la venta va a ser la misma. Nadie va a saber si primero salió la 1 o la 3, o al reves.
A men's basketball league assigns every player a two-digit number for the back of his jersey. If the league uses only the digits 1-5, what is the maximum number of players that can join the league such that no player has a number with a repeated digit (e.g. 22), and no two players have the same number?
A men's basketball league assigns every player a two-digit number for the back of his jersey. If the league uses only the digits 1-5, what is the maximum number of players that can join the league such that no player has a number with a repeated digit (e.g. 22), and no two players have the same number?
Combinación en grupos donde el orden SI importa, son digitos. No es lo mismo el dorsal 12 que el 21.
The security gate at a storage facility requires a five-digit lock code. If the lock code must consist only of digits from 1 through 7, inclusive, with no repeated digits, and the first and last digits of the code must be odd, how many lock codes are possible?
The security gate at a storage facility requires a five-digit lock code. If the lock code must consist only of digits from 1 through 7, inclusive, with no repeated digits, and the first and last digits of the code must be odd, how many lock codes are possible?
Permutation: Order matters. Furthermore we have restrictions on some digits. We use the Slot Method.
The Natural Woman, a women's health food store, offers its own blends of trail mix. If the store uses 4 different ingredients, how many bins will it need to hold every possible blend, assuming that each blend must have at least two ingredients? (Also assume that each bin can hold one and only one blend.)
The Natural Woman, a women's health food store, offers its own blends of trail mix. If the store uses 4 different ingredients, how many bins will it need to hold every possible blend, assuming that each blend must have at least two ingredients? (Also assume that each bin can hold one and only one blend.)
A pod of 6 dolphins always swims single file, with 3 females at the front and 3 males in the rear. In how many different arrangements can the dolphins swim?
A pod of 6 dolphins always swims single file, with 3 females at the front and 3 males in the rear. In how many different arrangements can the dolphins swim?
Multiple arrengement with two separate pools.
A delegation from Gotham City goes to Metropolis to discuss a limited Batman-Superman partnership. If the mayor of Metropolis chooses 3 members of the 7-person delegation to meet with Superman, how many different 3-person combinations can he choose?
Combinación en grupos donde el orden no importa. Nos da igual que el grupo este formado por Members 1, 3, 5 que Members 3,5,1. Las personas que van a componer el grupo son las mismas. Nadie va a saber si primero salio el miembro 1 o 3, o al reves. Distinto sería que De cuantas maneras pueden ir entrando a la reunión los grupos de tres miembros. De este modo si sería importante el orden y por lo tanto, la combinación seria 7!/4!=210 posibilidades.
A British spy is trying to escape from his prison cell. The lock requires him to enter one number, from 1-9, and then push a pair of colored buttons simultaneously. He can make one attempt every 3 seconds. If there are 6 colored buttons, what is the longest possible time it could take the spy to escape from the prison cell?
A British spy is trying to escape from his prison cell. The lock requires him to enter one number, from 1-9, and then push a pair of colored buttons simultaneously. He can make one attempt every 3 seconds. If there are 6 colored buttons, what is the longest possible time it could take the spy to escape from the prison cell?
The New York Classical Group is designing the liner notes for an upcoming CD release. There are 10 soloists featured on the album, but the liner notes are only 5 pages long, and therefore only have room for 5 of the soloists. The soloists are fighting over which of them will appear in the liner notes, as well as who will be featured on which page. How many different liner note arrangements are possible?
The New York Classical Group is designing the liner notes for an upcoming CD release. There are 10 soloists featured on the album, but the liner notes are only 5 pages long, and therefore only have room for 5 of the soloists. The soloists are fighting over which of them will appear in the liner notes, as well as who will be featured on which page. How many different liner note arrangements are possible?
Combinatoric in which order matters, because the soloists are assigned to different numbered pages, and they care in which page they are going to be.
The principal of a high school needs to schedule observations of 6 teachers. She plans to visit one teacher each day for a workweek (Monday through Friday), so she will only have time to see 5 of the teachers. How many different observation schedules can she create?
The principal of a high school needs to schedule observations of 6 teachers. She plans to visit one teacher each day for a workweek (Monday through Friday), so she will only have time to see 5 of the teachers. How many different observation schedules can she create?
A second grade class is writing reports on birds. The students' teacher has given them a list of 6 birds they can choose to write about. If Lizzie wants to write a report that includes two or three of the birds, how many different reports can she write?
A second grade class is writing reports on birds. The students' teacher has given them a list of 6 birds they can choose to write about. If Lizzie wants to write a report that includes two or three of the birds, how many different reports can she write?
A mother bird has 6 babies. Every time she returns to the nest, she feeds half the babies, even if some of those babies were fed the last time around. If it takes her 5 minutes to feed each baby, how long will it take her to feed all the possible combinations of three babies? leave out the time the mother bird spends away from the nest.
A mother bird has 6 babies. Every time she returns to the nest, she feeds half the babies, even if some of those babies were fed the last time around. If it takes her 5 minutes to feed each baby, how long will it take her to feed all the possible combinations of three babies? leave out the time the mother bird spends away from the nest.
Es confuso saber si el orden en el que va alimentando cada vez importa o no. En este caso entiende que no importa. Es interesante la frase "even if some of those babies were fed the last time around", para referirse a la necesidad de combinarlos.
Three gnomes and three elves sit down in a row of six chairs. If no gnome will sit next to another gnome and no elf will sit next to another elf, in how many different ways can the elves and gnomes sit?
Three gnomes and three elves sit down in a row of six chairs. If no gnome will sit next to another gnome and no elf will sit next to another elf, in how many different ways can the elves and gnomes sit?
Gordon buys 5 dolls for his 5 nieces. The gifts include two identical Sun-and-Fun beach dolls, one Elegant Eddie dress-up doll, one G.!. Josie army doll, and one Tulip Troll doll. If the youngest niece does not want the G.!. Josie doll, in how many different ways can he give the gifts?
Gordon buys 5 dolls for his 5 nieces. The gifts include two identical Sun-and-Fun beach dolls, one Elegant Eddie dress-up doll, one G.!. Josie army doll, and one Tulip Troll doll. If the youngest niece does not want the G.!. Josie doll, in how many different ways can he give the gifts?
Utilizar metodo de los anagramas cuando haya el mismo número de cosas que combinar que gente entre las que repartir.
In a bag of marbles, there are 3 red, 2 white, and 5 blue. If Bob takes 2 marbles out of the bag, what is the probability that he will have one white and one blue marble?
In a bag of marbles, there are 3 red, 2 white, and 5 blue. If Bob takes 2 marbles out of the bag, what is the probability that he will have one white and one blue marble?
A florist has 2 azaleas, 3 buttercups, and 4 petunias. She puts two flowers together at random in a bouquet. However, the customer calls and says that she does not want two of the same flower. What is the probability that the florist does not have to change the bouquet?
A florist has 2 azaleas, 3 buttercups, and 4 petunias. She puts two flowers together at random in a bouquet. However, the customer calls and says that she does not want two of the same flower. What is the probability that the florist does not have to change the bouquet?
Five A-list actresses are vying for the three leading roles in the new film,
Five A-list actresses are vying for the three leading roles in the new film, "Catfight in Denmark." The actresses are Julia Robards, Meryl Strep, Sally Fieldstone, lauren Bake-all, and Hallie Strawberry. Assuming that no actress has any advantage in getting any role, what is the probability that Julia and Hallie will star in the film together?
A polling company reports that there is a 40% chance that a certain candidate will win the next election. If the candidate wins, there is a 60% chance that she will sign Bill X and no other bills. If she decides not to sign Bill X, she will sign either Bill Y or Bill Z, chosen randomly. What is the chance that the candidate will sign Bill Z?
A polling company reports that there is a 40% chance that a certain candidate will win the next election. If the candidate wins, there is a 60% chance that she will sign Bill X and no other bills. If she decides not to sign Bill X, she will sign either Bill Y or Bill Z, chosen randomly. What is the chance that the candidate will sign Bill Z?
In the town of Z, the town lion roars on some days and not on others. If a day is chosen at random from last March, what is the probability that on that day, either the town lion roared or it rained? (1) last March, the lion never roared on a rainy day. (2) Last March, the lion roared on 10 fewer days than it rained.
In the town of Z, the town lion roars on some days and not on others. If a day is chosen at random from last March, what is the probability that on that day, either the town lion roared or it rained? (1) last March, the lion never roared on a rainy day. (2) Last March, the lion roared on 10 fewer days than it rained.
For one roll of a certain die, the probability of rolling a two is 1/6. If this die is rolled 4 times, which of the following is the probability that the outcome will be a two at least 3 times? (A) (1/6)4 (8) 2(1/6i + (1/6)4 (C) 3{1/6)3(5/6) + (1/6)4 (O) 4{1/6)3{5/6) + (1/6)4 (E) 6{1/6)3{5/6) + (1/6)4
For one roll of a certain die, the probability of rolling a two is 1/6. If this die is rolled 4 times, which of the following is the probability that the outcome will be a two at least 3 times? (A) (1/6)4 (8) 2(1/6i + (1/6)4 (C) 3{1/6)3(5/6) + (1/6)4 (O) 4{1/6)3{5/6) + (1/6)4 (E) 6{1/6)3{5/6) + (1/6)4
A zoo has w wildebeests, y yaks, z zebras, and no other animals. If an animal is chosen at random from the zoo, is the probability of choosing a yak greater than the probability of choosing a zebra? (1) y/(w+ z) > 1/2 (2) z/(w+ y) < 1/2
A zoo has w wildebeests, y yaks, z zebras, and no other animals. If an animal is chosen at random from the zoo, is the probability of choosing a yak greater than the probability of choosing a zebra? (1) y/(w+ z) > 1/2 (2) z/(w+ y) < 1/2
A miniature gumball machine contains 7 blue,S green, and 4 red gumballs, which are identical except for their colors. If the machine dispenses three gumballs at random, what is the probability that it dispenses one gumball of each color?
A miniature gumball machine contains 7 blue,S green, and 4 red gumballs, which are identical except for their colors. If the machine dispenses three gumballs at random, what is the probability that it dispenses one gumball of each color?
Lo he resuelto de manera diferente. 1.- Cálculo de todos las posibles combinaciones de tres: 16!/(3!13!)= 560. 2.- Los posibles outcomes de cada uno de los colores: 7x5x4=140. 140/560=1/4
Kate and her twin sister Amy want to be on the same relay-race team. There are 6 girls in the group, and only 4 of them will be placed at random on the team. What is the probability that Kate and Amy will both be on the team?
Kate and her twin sister Amy want to be on the same relay-race team. There are 6 girls in the group, and only 4 of them will be placed at random on the team. What is the probability that Kate and Amy will both be on the team?
No se resuelve mediante el Glue Method.
Three small cruise ships, each carrying 10 passengers, will dock tomorrow. One ship will dock at Port A, another at Port B, and the third at Port C. At Port A, two passengers will be selected at random; each winner will receive one gift certificate worth $50. At Port B, one passenger will be selected at random to receive a gift certificate worth $35, and at Port C, one passenger will be selected at random to receive a gift certificate worth $25. How many different ways can the gift certificates be given out?
Three small cruise ships, each carrying 10 passengers, will dock tomorrow. One ship will dock at Port A, another at Port B, and the third at Port C. At Port A, two passengers will be selected at random; each winner will receive one gift certificate worth $50. At Port B, one passenger will be selected at random to receive a gift certificate worth $35, and at Port C, one passenger will be selected at random to receive a gift certificate worth $25. How many different ways can the gift certificates be given out?
Combination
Is a selection of items from a larger pool. In a combination, the order of items does not matter. In other words, the three-item combinations of items A-B-C and B-C-A are considered identical. Think teams or groups: all that matters is who is in and who is out. The winners are considered indistinguishable. n! ----------- r! · (n-r)!
Pemutation
Is a selection of items from a larger pool. In a permutation, however, the order of items matters. In other words, the permutations A-B-C and B-A-C are considered distinct. Think seating arrangements or Olympic medal ceremonies: what matters is not only who gets a seat or a medal, but also lYhi91 seat or medal each winner gets. The winners are considered distinguishable. n! ----------- (n-r)!
A medical researcher must choose one of 14 patients to receive an experimental medicine called Progaine. The researcher must then choose one of the remaining 13 patients to receive another medicine, called Ropecia. Finally, the researcher administers a placebo to one of the remaining 12 patients. All choices are equally random. If Donald is one of the 14 patients, what is the probability that Donald receives either Progaine or Ropecia?
The "textbook" approach to this problem-finding the total number of different distributions giving either Progaine or Ropecia to Donald, and then dividing that number by the total number of distributions--can be time-consuming. Instead, notice the symmetry of the problem. None of the 14 patients is "special" in any way, so each of them must have the same chance of receiving Progaine or Ropecia. Since Progaine is only administered to one patient, each patient (including Donald) must have probability 1/14 of receiving it. The same logic also holds for Ropecia. Since Donald cannot receive both of the medicines, the desired probability is the probability of receiving Progaine, plus the probability of receiving Ropecia: 1/14 + 1/14 = 1/7. The placebo is irrelevant, as is the order that the researcher artificially chose for the selection process. You can solve this problem by using a sequence of two choices (Progaine or not; if not, then Ropecia or not). But it is faster to use a symmetry argument.
A gambler rolls three fair six-sided dice. What is the probability that two of the dice show the same number, but the third shows a different number?
A gambler rolls three fair six-sided dice. What is the probability that two of the dice show the same number, but the third shows a different number?
Jill is dividing her ten-person class into two teams of equal size for a basketball game. If no one will sit out, how many different match-ups between the two teams are possible? 10 25 126 252 630
Correct Answer: (C) This is a trickier spin on a basic combinatorics problem. Begin by asking how many groups of 5 can be created from a pool of 10 candidates. Order does not matter, so this is a combinations problem. Use the combinations formula: n!/(k!)(n-k)! That answer would be 10!/[(5!)(5!)] = 252. But (D) is a trap answer. The problem does not ask how many team arrangements are possible; it asks how many match-ups are possible. Each match-up consists of a team of five opposing the remaining five people. Therefore, each match-up involves two of the 252 teams. To find the number of match-ups, divide 252 in half for a total of 126. The correct answer is (C).
Five people - Arun, Benji, Claire, Diana and Earl - are to be seated on a bench in a movie theater. If Arun and Benji must be seated at the ends of the bench, and Claire and Earl refuse to be seated next to each other, how many orders can then sit in to satisfy all the above conditions?
Solution: D. A and B must be seated at the ends so in two ways we can arrange. A _ _ _ B or B _ _ _ A = 2 ways And C and E cannot be seated together so we can denote their positions as either: _ C _ E_ or _ E _ C_ = 2 ways The middle person has to be D so only one way. Hence the number of ways = 2 * 2 *1 = 4 making D the correct answer.